백준 1504번 - 특정한 최단 경로

풀이과정

다익스트라 X 3

성공 1000ms
u,v 노드를 거치면서 1,N 노드를 가는 방법은 결국에 2가지이다.

1 -> u -> v -> N
1 -> v -> u -> N
그래서 가장 먼저 떠오르는 생각은 1,u,v 를 시작으로 하는 각각의 최단경로를 구한 다음에, 1 -> u + v -> N , 1 -> v + u -> N 중 작은 값을 구하는 식으로 접근했다.
dijkstra를 3번이나 해야하기 때문에 그다지 효율적이라고 생각하지는 않았지만, n이 비교적 작기 때문에 시간 복잡도를 초과하지 않을 것 같아서 진행했다.

코드

import sys
import heapq

n, e = map(int, input().split())
INF = int(1e9)
distance = [INF] * (n + 1)
graph = [[INF for i in range(n + 1)] for j in range(n + 1)]

for _ in range(e):
    a, b, c = list(map(int, sys.stdin.readline().split()))
    graph[a][b] = c
    graph[b][a] = c

u, v = map(int, input().split())

def dijkstra(start):
    heap = []
    distance[start] = 0
    heapq.heappush(heap, (0, start))
    while heap:
        dis, node = heapq.heappop(heap)
        for i, dis in enumerate(graph[node]):
            if i != 0 and i != node and dis != INF:
                new_dis = distance[node] + dis
                if distance[i] > new_dis:
                    distance[i] = new_dis
                    heapq.heappush(heap, (new_dis, i))

dijkstra(1)
s_u, s_v = distance[u], distance[v]

distance = [INF] * (n + 1)
dijkstra(u)
u_v, u_e = distance[v], distance[n]

distance = [INF] * (n + 1)
dijkstra(v)
v_e = distance[n]

result = min(s_u + u_v + v_e, s_v + u_v + u_e)
if result >= INF:
    print(-1)
else:
    print(result)

약간의 개선

생각해보니 방향성 그래프가 아니므로 1번 노드를 시작으로 하는 최단경로 계산은 필요없다.
3번의 연산에서 2번으로 줄일 수 있다.!
880ms 로 줄었다. ㅋㅋㅋ

1등먹기

더 나은 방법이 없는지 궁금해서 해당 문제를 제출한 사람 중 python으로 문제를 푼 사람의 코드를 봤다.
이분도 3번의 최단경로 계산이 포함되어 있었다.
약간의 개선으로 2번으로 줄이면 내가 1등으로 올라갈 수 있을 것 같았다.

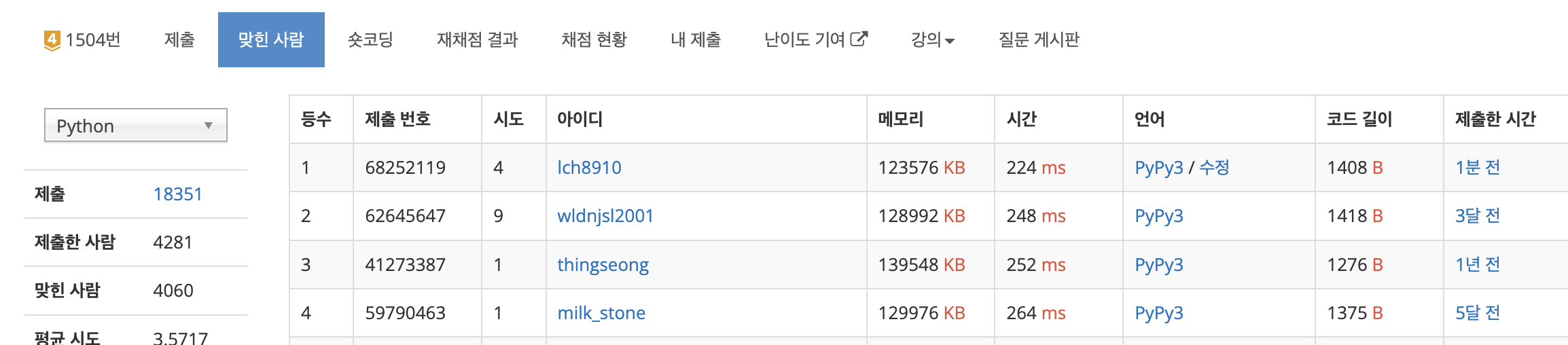
2번으로 줄이고 제출하니 1등으로 올라갈 수 있었다.